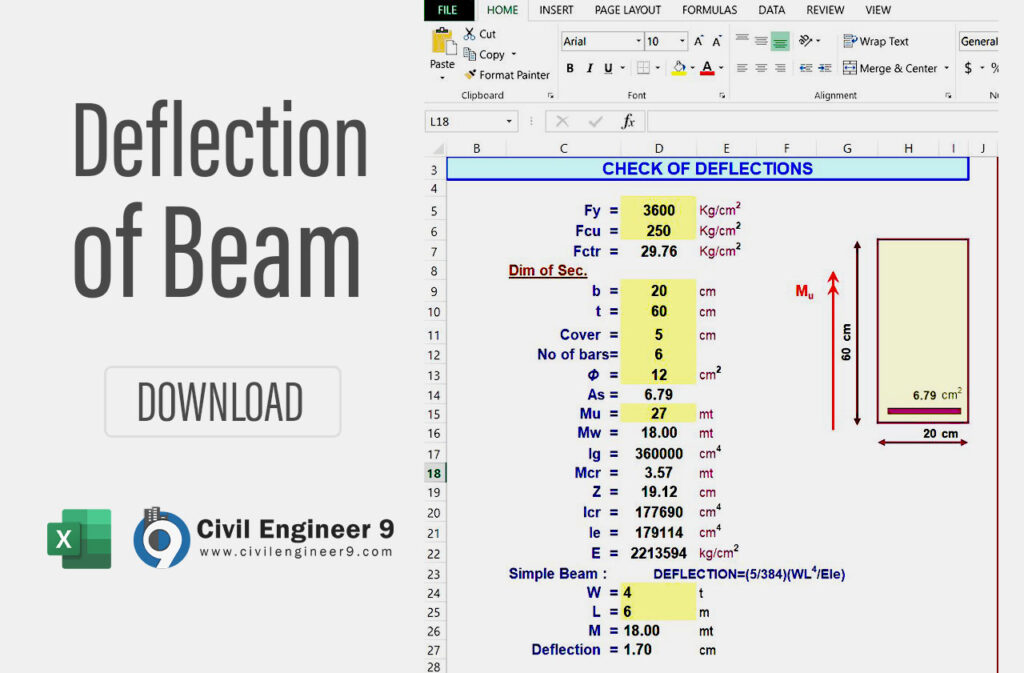
With this spreadsheet, you can calculate deflection of beam and check or determine the value for the safe design. Before this, you need to design the beam.
In this Beam Design Excel Sheet, you can easily calculate the flexural reinforcement and shear reinforcement in beams.
Related Download:
- Design Of Shear Reinforcement for Beam
- T Beam Design
- Beam Reinforcement Details
- Cantilever Beam Reinforcement Details
Calculate Deflection of Beam
The deflection of a beam can be described in terms of its slope and curvature, which indicate the angle and radius of curvature of the deflected shape, respectively. Deflection is an important factor to consider in the design of structures and mechanical systems, as excessive deflection can lead to failure or instability.
Beam deflection formula
The deflection of a beam is typically calculated using one of several analytical formulas that have been developed based on beam theory. The specific formula used depends on the geometry of the beam, the boundary conditions, and the distribution of the applied loads.
Here are a few examples of commonly used beam deflection formulas:
- For a simply supported beam with a uniformly distributed load:
δ = (wL^4)/(8EI)
where δ is the deflection of the beam at the center, w is the uniformly distributed load, L is the length of the beam, E is the modulus of elasticity of the beam material, and I is the moment of inertia of the beam’s cross-sectional area.
- For a cantilever beam with a point load at the end:
δ = (PL^3)/(3EI)
where δ is the deflection of the beam at the end, P is the magnitude of the point load, L is the length of the beam, E is the modulus of elasticity of the beam material, and I is the moment of inertia of the beam’s cross-sectional area.
- For a simply supported beam with a point load at the center:
δ = (PL^3)/(48EI)
where δ is the deflection of the beam at the center, P is the magnitude of the point load, L is the length of the beam, E is the modulus of elasticity of the beam material, and I is the moment of inertia of the beam’s cross-sectional area.
Note that these formulas are based on certain assumptions and simplifications, and may not be accurate for all types of beams and loading conditions. More complex beam deflection formulas and numerical methods, such as the finite element method, may be required for more accurate results.
Download Excel Sheet to Calculate Deflection of Beam
Here is provided for free download Excel sheet to calculate deflection of beam and check.
Deflection of Beam